Orbitale Freiheitsgrade

 

Die geometrische Anordnung von elektronischen Wellenfunktionen im Festkörpergitter stellt einen wichtigen Freiheitsgrad dar. Er zeigt sich in den CEF-Niveaus (CEF=Crystalline Electric Field) weitgehend lokalisierter 3d- und 4f-Elektronen, die unter bestimmten Bedingungen zu gemischt elektronisch/strukturellen Instabilitäten führen können. Als kooperativer Jahn-Teller-Phasenübergang, der zu einer kohärenten Verzerrung des Festkörpergitter führt, wurden dieser Effekte schon vor vielen Jahren untersucht.

 

Neue Aktualität gewinnt diese Thematik durch Manganate mit hohem Magnetowiderstand, Ordnung von 4f-Quadrupolmomenten in intermetallischen Seltenerdverbindungen sowie Beobachtung einer Orbitalflüssigkeit in La-Titanat.

 

In den Maganaten (La1-x,Cax)MnO3 mit Perowskitstruktur führt eine tetragonale Gitterverzerrung der Sauerstoffumgebung um ein Mn3+-Ion zu einer Aufhebung der energetischen Entartung der elektronischen Orbitale. Entsprechend ordnen sie sich im Raum an. Das Verhältnis der Stöchiometrie La/Ca stellt einerseits über das Verhältnis Mn3+/Mn4+ die Besetzung der eg-Orbitale ein, andererseits ändert es das Volumen der Einheitszelle.

 

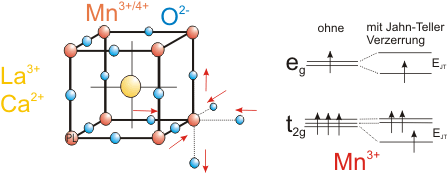
Perowskitstruktur mit tetragonaler Jahn-Teller-Verzerrung und daraus folgender Modulation der 3d-Kristallfeldniveaus des Mn3+.

 

Aus dem Wechselspiel von Gitterverzerrung, magnetischer Wechselwirkung und Hüpfen der Elektronen (Doppelaustausch) folgt ein reichhaltiges Phasendiagramm mit antiferromagnetischen, ferromagnetischen und ladungsgeordneten Phasen.

 

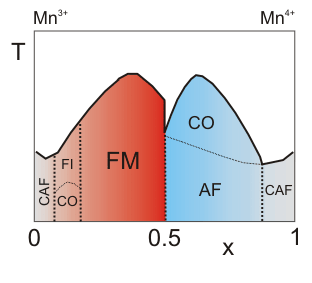
Schematisches Phasendiagramm für La1-xCaxMnO3 mit verkantetem Antiferromagneten (CAF), ferromagnetischem Isolator (FI), ladungsgeordneter Phase (CO) und metallischem Ferromagneten (FM).

 

Diese Phasendiagramme lassen sich nur verstehen, wenn die Ausrichtung der elektronischen Wellenfunktionen des 3d-Elektrons, also die orbitalen Freiheitsgrade, Berücksichtigung finden.

 

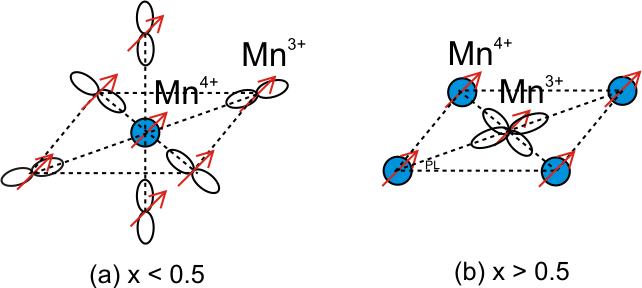
Modelle der Ordnung von Spin (rote Pfeile), Orbital (eg-"Gurke") und Ladung (Mn4+:blauer Kreis) in Abhängigkeit von der Dotierung x in (La1-x,Cax)MnO3 [M. Mizokawa, et al.].

 

Zur Zeit interessiert man sich für die direkte Spektroskopie von orbitalen Anregungen, dynamischen orbitalen Fluktuationen sowie elektronischen Phasendiagrammen alternativer Übergangsmetallverbindungen, die sich nur unter Berücksichtigung dieses Freiheitsgrads beschreiben lassen. Für mich ist besonders der erstere Punkt von Interesse.

 

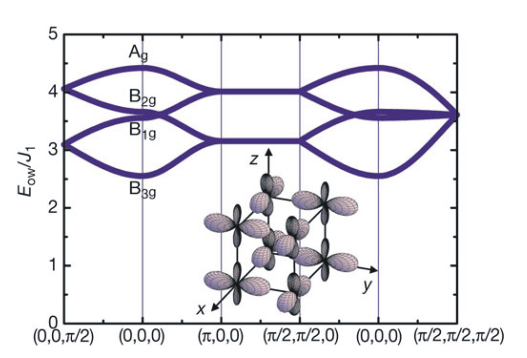
Dispersion und schematische Illustration von orbitaler Ordnung in LaMnO3 [Saitoh, et al, Nature]. Eine typische Energieskala dieser Anregungen ist eine Austauschkonstante J1, die Pseudospin- Operatoren T besetzter eg-Orbitale verknüpft. Die dazugehörigen Quantenzahlen bezeichnen die Besetzung eines 3z2-r2 oder eines x2-y2-Orbitals. Diese Energieskala beträgt in Manganaten ca. 500K.

 

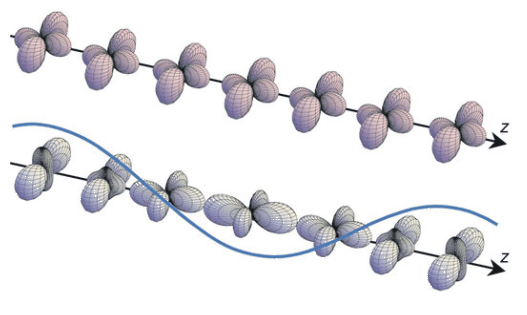
Schematische Illustration von orbitalen Anregungen mit dem Grundzustand und einer orbitale Welle, die im Festkörper propagiert [Saitoh, et al, Nature].

 

Die orbitalen Anregungen können als Quasiteilchen mittels optischer Spektroskopie untersucht werden. Ihre Energie und Dispersion hängt natürlich von der untersuchten Ladungs-, Moment und Orbitalverteilung im Raum und somit besonders von der Temperatur der Probe ab. In einer Veröffentlichung der Arbeitsgruppen um Y. Tokura, Tokyo und S. Maekawa, Sendai wurde dies kürzlich demonstriert.

 

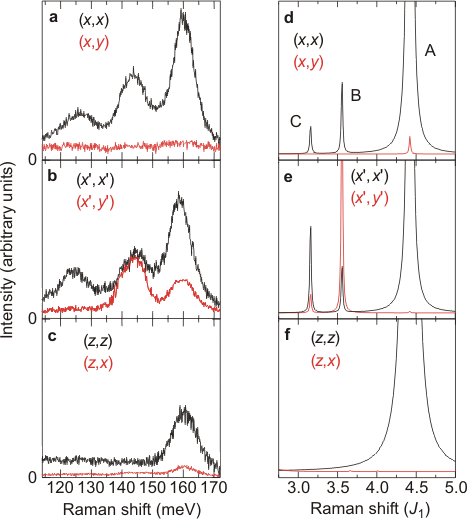
(a-c) Raman-Experiment und (d-f) Modellrechnung zu orbitalen Anregungen in LaMnO3 [Saitoh, et al, Nature]. Es werden drei Moden bei 1000, 1160 und 1280cm-1 bei tiefen Temperaturen (T=9K) beobachtet. Die Übereinstimmung mit der Theorie ist beeindruckend. Für höhere Temperaturen verschieben die Moden zu niedrigeren Frequenzen und verlieren Intensität.

 

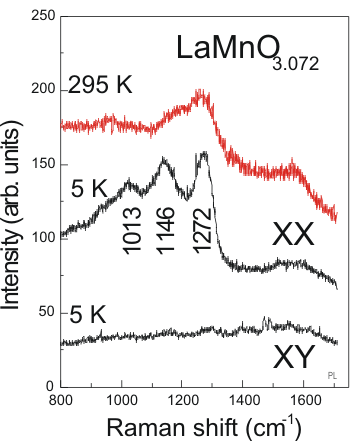
Raman-Experimente der Aachener Lichtstreugruppe in Zusammenarbeit mit V. Gnezdilov und Y. Pashkevich an einer Probe mit Sauerstoff-Überschuss präpariert von S. Barilo.

 

Bei unseren Experimenten in Aachen wurden Hinweise auf eine möglicherweise nur schwache Abhängigkeit der Moden von der Dotierung gesammelt. Eine eindeutige Diskriminierung dieser Signale von zwei-Phonon-Streuung in einem vergleichbaren Frequenzbereich erscheint und weiterhin wichtig. Weitere Experimente werden zur Zeit an Manganaten verschiedener Dotierung durchgeführt.

 

Eine weitere wichtige Verbindung zur Themenstellung "orbitale Freiheitsgrade" ist das Titanat LaTiO3 mit der Elektronenkonfiguration des Ti3+ von 3d1 in einer Perowskitstruktur. Diese Verbindung ist undotiert (La1-xSrxTiO3+d, x=0, d=0) ein langreichweitig antiferromagnetisch geordneter Isolator. In der Neutronenstreuung beobachtet für man T<TN=132K recht konventionelle Magnonenzweige und mit einem etwas reduzierten geordnetes Moment (m=0.45mB). Ein geordnetes reines Spinmoment würde m=0.85mB entsprechen. Die Daten lassen sich gut mit einem isotropen s=1/2 Heisenberg-System auf einem einfachen kubischen Gitter und einer Austauschkopplungskonstante J=180K beschreiben. Das sehr kleine, durch Spinverkantung erzeugte unkompensierte Moment (10-2mB) und die sehr kleine Anisotropielücke durch antisymmetrische Dzyaloshinskii-Moriya Wechselwirkung spielen dabei nur eine untergeordnete Rolle [B. Keimer, et al., PRL (2000)].

 

Überraschend ist allerdings der fehlende Beitrag des orbitalen Moments. Da in Strukturuntersuchungen keine statische Jahn-Teller-Verzerrung beobachtet werden kann, sollte man von einer Spin-Bahn-induzierten Aufspaltung der t2g-Multiplets (kubisches Kristallfeld) in einen vierfach entarteten Grundzustand und ein höher liegendes Kramers-Dublett ausgehen. Dieser Grundzustand entspricht einem ungequentschten Orbital- oder Bahnmoment, das vergleichbar groß und antiparallel zum Spinmoment ausgerichtet sein sollte. Weder die erwartete Anisotropie, noch ein kompensiertes Moment werden experimentell beobachtet.

 

Ein ähnliches Verhalten zeigen verdünnte Ti3+-Ionen in einer Perowskit-Matrix. Aus ESR-Experimenten kann man hier recht isotrope g-Faktoren ableiten, die einem dynamischen Jahn-Teller-Effekt zugeschrieben wurden. Die Aufhebung der Orbitalentartung basiert hier auf einer Kopplung an Phonon-Nullpunktsschwingungen [siehe Referenzen in B. Keimer, et al.]. Diese Vorstellung hat eine Parallele zum Kondo-Effekt, der dynamischen Abschirmung eines lokalisierten magnetischen Moments durch Hybridisierung mit Leitungselektronen. Er führt zu einer Aufhebung der Spinentartung und einem Singulett-Grundzustand, der mit langreichweitiger magnetischer Ordnung konkurriert.

 

Da es für die "konzentrierte" Verbindung LaTiO3 keine eindeutige Evidenz für eine kooperative Verzerrung gibt, wurde vorgeschlagen, dass der orbitalen Freiheitsgrad dynamisch gequenscht ist und in einer orbitalen Flüssigkeit vorliegen. In einem Modell von Kkaliullin und Maekawa wird dies beschrieben [Khaliullin, et al., PRL (2000)]. Es beruht auf einer Quantenresonanz zwischen Niveaus, die die orbitale Entartung durch die Bildung von orbitalen RVB-Zuständen aufhebt. Antiferromagnetische Ordnung mit leicht reduziertem Moment steht nicht im Widerspruch zu diesem Zustand, da Magnonen in der Nähe des Zonenrands an der lokalen Resonanz teilhaben und so zu kombinierten Spin-Orbital-Anregungen führen.

 

Weiterführende Literatur: The cooperative Jahn-Teller-Effects, G.A. Gehring und K.A. Gehring, Rep. Progress in Phys. 38, 1 (1975). Orbital Liquid in Perovskite Transition-Metal Oxides, S. Ishihara, M. Yamanaka und N. Nagaosa, PRB 56, 686 (1997). Magnetic Phases to Order, N. Mathur, Nature 400, 405 (1999). Metal-Insulator Transitions, M. Imada, A. Fujimori, Y. Tokura, Rev. Mod. Physics 70, 1039 (1998). Charge and Orbital Ordering in (La,Sr)MnO3, T. Mizokawa, D.I. Khomskii und G.A. Sawatzky, PRB 61, R3776 (2000). Orbital Polarons and Ferromagnetic Insulators in Magnanites, T. Mizokawa, D.I. Khomskii und G.A. Sawatzky, PRB 63, 24403 (2001).  Observation of Orbital Waves as Elementary Excitations in a Solid, E. Saitoh, et al., Nature 410, 180 (2001). Spin Dynamics and Orbital State in LaTiO3, B. Keimer, et al., PRL 85, 3946 (2000). Orbital Liquid in Three-Dimensional Mott Insulator: LaTiO3, G. Khaliullin und S. Maekawa, PRL 85, 3950 (2000).