Spin-Frustration und konkurrierende Wechselwirkungen

 

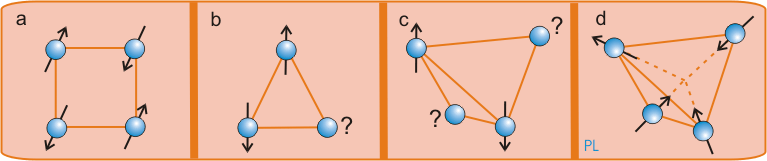
Frustration charakterisiert ein System dessen konkurrierende Wechselwirkungen in einem mögliche Grundzustand nicht gleichzeitig befriedigt werden können. Ein wichtiges Beispiel stellen antiferromagnetische Spinwechselwirkungen lokalisierter Spins dar, die je nach geometrischer Anordnung und Reichweite der Wechselwirkung zu Spin-Frustration führen. Die untere Abbildung zeigt Beispiele für frustrierte Spin-Topologien. Das Quadratgitter ist frustriert, wenn auch antiferromagnetische Wechselwirkungen zu übernächsten Nachbarn (in der Diagonale) berücksichtigt werden. Eine weitere Ursache für Frustration stellt Unordnung dar, die in klassischen magnetischen Systemen bei tiefen Temperaturen zu einem Spinglas führt.

 

Spinfrustration auf antiferromagnetisch gekoppelten (a) Quadratgittern, (b) 2D Dreiecksgittern, (c) 3D Tetraedern und (d) ein Kompromiss-Grundzustand eines klassischen Spin-Tetraeders mit Anisotropien.

 

In klassischen Spinsysteme führen Frustration und konkurrierende Wechselwirkungen zu einer erhöhten Entartung der niedrigenergetischen Zustände und Nullpunkts-Entropie.  Dies führt z.B. in der spezifischen Wärme cp(T) zu Potenzgesetzen. In einem langreichweitig geordneten AF wird statt dessen ein exponentieller Abfall (Anisotropielücke des AF) beobachtet. Bei vergleichsweise tiefen Temperaturen existiert eine Neigung zu Spinglas- oder Spincluster-Übergängen. Als ein Maß für die Frustration kann aus magnetischen Messungen das Verhältnis der Curie-Weiss-Konstante zur Ordnungstemperatur abgeleitet werden.

 

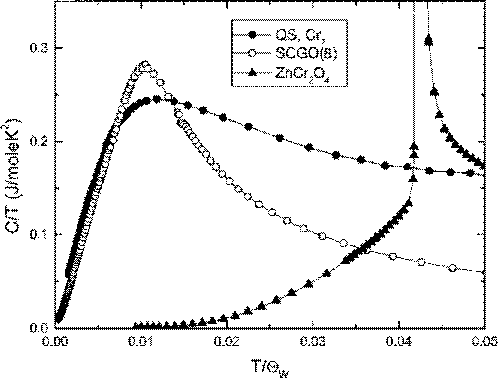
Spezifische Wärme c/T(T) von verschiedenen Kagome-Systemen. Das Spinell ZnCr2O4 zeigt eine durch Neel-Ordnung verursachte Anomalie bei 0,043 QCW und danach einen schnellen Abfall [I.S. Hagemann, et al. PRL (2001)].

 

In dieser Tabelle werden Vertreter der Spinelle und verknüpfte Kagome-Gitter verglichen. Im Allgemeinen gilt: QCW>>TN. Das Verhältnis QCW>>TN steigt mit reduzierter Kopplung der Tetraeder bzw. Kagome-Ebenen drastisch an.

 

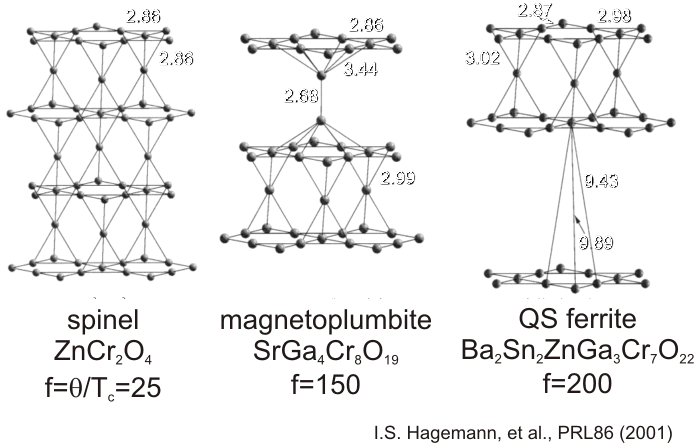
Spintopologie einiger  Spinell- und Kagome-Verbindungen. Wichtige Bindungslängen sind angegeben [I.S. Hagemann, PRL86 (2001)].

 

Diese Situation ändert sich in vielen S=1/2 Systemen, die wegen des kleinen Spins und fehlenden Anisotropien ausgeprägte Quantenfluktuationen aufweisen. Hier werden unmagnetische Singulett- oder RVB-Grundzustände bevorzugt, die den Charakter einer Spinflüssigkeit, häufig mit Spingap oder Pseudogap, besitzen. Der RVB-Zustand wurde schon 1973 von P.W. Anderson als Alternative zum klassischen Neel-Zustand vorgeschlagen. Spin-Frustration begünstigt diese Tendenz, da sie zu einer Lokalisierung der Anregungen führt. Scheinbar kleine Änderungen der Kopplungsparameter führen über einen quantenkritischen Punkt in konkurrierende, langreichweitig geordnete Phasen.

 

1D-Spinketten mit nichtlinearem Superaustausch und nächste-Nachbarn-WW.: CuGeO3, SrCuO2 2D-Shastry-Sutherland-Gitter SrCu2(BO3)2, 2D-Kagome-Netzwerk Ba2Sn2ZnGa3Cr7O22 schwach gekoppelte Spin-Tetraeder oder Spin-Plaketten: Cu2Te2O5Br2 und CaV4O9 3D stark gekoppelte, eckenverknüpfte Spin-Tetraeder: Kagome-Systeme und 2D-Dreiecksgitter, SrCr8Ga4O19, Spinell, Pyrochlore (bezeichnen verschiedene Stapelfolgen oder Verknüpfungen von Dreiecksgittern).

 

Weitere Aspekte: interessantes Wechselspiel: Frustration ("Underconstraint") vs. z (Koordinationszahl) vs. Dimensionalität. Frustration führt zu kollektiven Anregungen in Systemen mit Spingap mit sehr niedrigen Energien: "gebundene Zustände" Frustration oder konkurrierende WW. sind oft mit quantenkritischen Punkten verbunden, bei denen für T=0 konkurrierende Zustände energetisch entartet sind. Frustration durch orbitale Freiheitsgrade (Ausrichtung und Besetzung von 3d-Wellenfunktionen) wird noch fortgeführt......

 

Weiterführende Literatur:  Geometrically Frustrated Magnetic Materials, J.E. Greendan, J. Mater. Chem. 11, 37-53 (2001).  (most recent Review) Frustration in Magnetic Systems, A.P. Ramirez, Annu. Rev. Mat. Sci. 24, 453 (1994). (Review) Recent Experimental Progress in the Study of Geometrical Magnetic Frustration, P. Schiffer, A.P. Ramirez, Comments Cond. Mat. Phys. 18, 21 (1996). (Review) P.W. Anderson, Phys. Rev. 102, 1008 (1956) und Mater. Res. Bull. 8, 153 (1973). Ga NMR Study of the Local Susceptibility in the Kagome-Based SrCr8Ga4O19, P. Mendels, et al., PRL85, 3496 (2000). Geometric Magnetic Frustration in Ba2Sn2Ga3ZnCr7O22: A Two-Dimensional Spinel Based Kagome Lattice, I.S. Hagemann, et al., PRL 86, 894 (2001). Spin-Driven Jahn-Teller Distortion in a Pyrochlore System, Y. Yamashita, K. Ueda, PRL 85, 4960 (2000). Magnetism of a tetrahedral cluster-chain, W. Brenig, K.W. Becker, P. Lemmens, cond-mat/0101460.