Quantenkritisches Verhalten und konkurrierende Zustände

 

In Quanten-Spinsystemen kann durch eine Änderung eines Parameters ein Übergang zwischen konkurrierenden Grundzuständen induziert werden. In niedrigdimensionalen Systemen kann dies ein Übergang von einer Spinflüssigkeit mit kurzreichweitigen Dimer-Korrelationen (Bild unten links) in einen Neel-artigen langreichweitig geordneten Grundzustand (unten rechts) sein. Die Anregungen dieser beiden konkurrierenden Zuständen sind grundverschieden, ihre Grundzustandsenergie allerdings bei T=0 entartet.

 

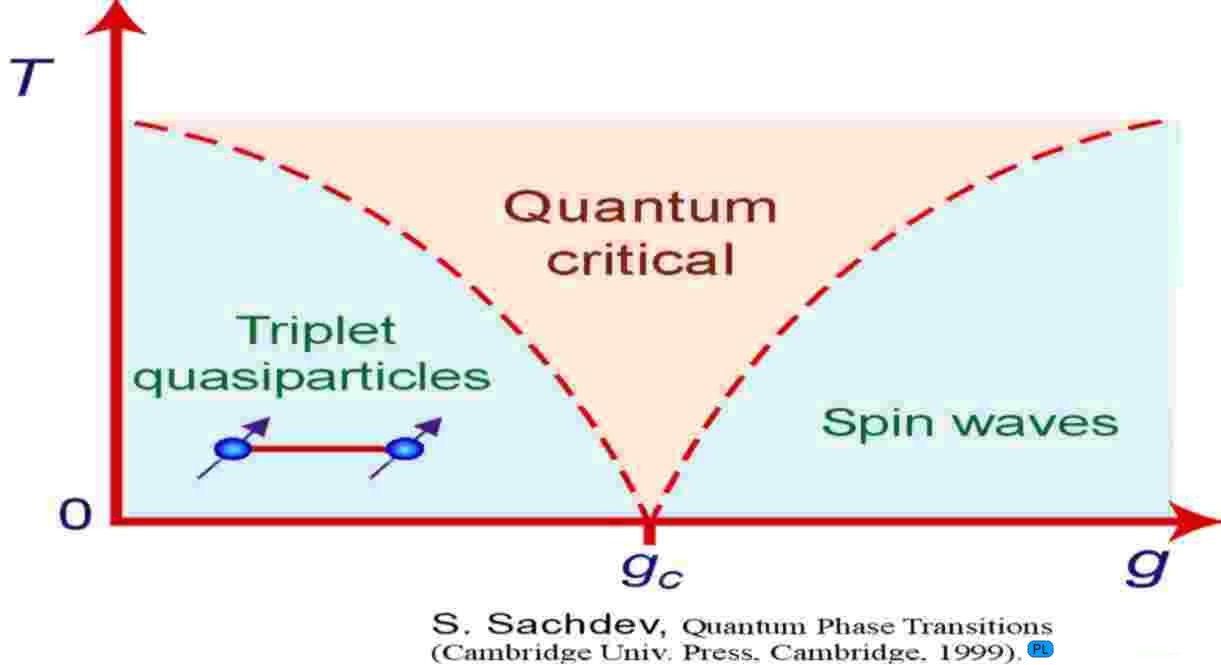
Der bei T=0 gegebene quantenkritische Punkt wird von Quantenfluktuationen dominiert. Die verallgemeinerte Kopplungskonstante g kann z.B. das Verhältnis von zwei Kopplungskonstanten (g=J1/J2) innerhalb und zwischen Spin-Plaketten sein. Dotierung mit mobilen Ladungsträgern und seltsame Spin-Topologien können diese unstetigen Übergänge induzieren. Wir haben in den letzten Jahren besonders in Einfluss von Frustration, also konkurrierenden Austauschwechselwirkungen, untersucht.

 

Phasendiagramm eines Quanten-Spinsystems, dass durch eine Kopplungsstärke g charakterisiert wird. [S. Sachdev, Quantum Phase Transitions]

 

Besonders interessant ist der Fall endlicher kleiner Temperaturen für g=gc, der quantenkritische Bereich. Hier "mischen" die Zustände und die Konkurrenz wird teilweise aufgehoben, was zu seltsamen Potenzverhalten der kritischen Größen führt. Das Anregungsspektrum solcher Systems im quantenkritischen Bereich mit ihren kollektiven Anregungen und gebundenen Zustände ist sowohl theoretisch als auch experimentell erst wenig untersucht, verspricht aber besonders signifikante Ergebnisse.

 

Die theoretische Beschreibung quantenkritischen Verhaltens ist sehr eng mit einer Theorie für quantenmechanische Systeme mit unendlich vielen Freiheitsgraden verknüpft, der Quantenfeldtheorie. Dabei wird ein System mit D Raumdimensionen durch ein Problem der statistischen Physik mit (D+1) Dimensionen ersetzt. Die Rolle der Temperatur des statistischen Problems übernimmt dabei eine Kopplungskonstante, die Stärke von Quantenfluktuationen misst, während die Temperatur des quantenmechanischen Problems als inverse Längenskala einer imaginären Zeitachse eingeht.

 

Phasenübergänge zwischen geordneten und ungeordneten Zuständen werden durch die spontane Brechung einer Symmetrie erzwungen. An einem kontinuierlichen Übergang konkurrieren diese beiden kollektiven Zustände und diese Konkurrenz ist auf allen Skalen (bis zu einem cut-off bei kleinen Längen) gleich. Das System ist jetzt selbstähnlich, endsprechend einem algebraischen Abfall der Korrelationsfunktionen und dynamischen Response (x-n). Der quantenkritische Punkt kann in einem System für T=0 induziert werden, wenn die Stärke der Quantenfluktuationen kontinuierlich eingestellt werden kann.

 

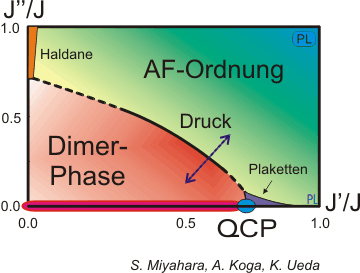
Verbindungen, die gute Kandidaten für dieses Szenario darstellen sind die zweidimensionalen Quanten-Spinsysteme CaV4O9 und SrCu2(BO3)2. Die letztere Verbindung soll besonders nahe an einem quantenkritischen Punkt (QCP) liegen. Experimente unter Druck können möglicherweise einen Quanten-Phasenübergang induzieren. Dabei soll zusätzlich zur Interdimer-Kopplung J' auch eine dreidimensionale Zwischenschicht-Kopplung J'' eine Rolle spielen. Eine experimentelle Verifikation steht hier leider noch aus.

 

Postuliertes Tieftemperatur-Phasendiagramm der Verbindung SrCu2(BO3)2. Das Verhältnis J'/J bestimmt die Wechselwirkung in der Ebene der Dimere, während J''/J die Wechselwirkung zwischen den Ebenen charakterisiert. Unter Normaldruck befindet sich SrCu2(BO3)2 in der Dimer-Phase.

 

Auch für Hochtemperatur-Supraleitung wird dieses Szenario diskutiert. Hier liegt der quantenkritische Punkt im Dotierungsphasendiagramm bei maximaler supraleitender Ordnungstemperatur und entspricht der Brechung einer "verborgenen Ordnung". Diese wird z.B. von P. Lee im Rahmen einer SU(2) Eichtheorie als Flussphase beschrieben, während M. Fischer von topologischen Defekten in einer Ising (Z2) Eichtheorie ausgeht. Im letzteren Ansatz finden sich möglicherweise die in einigen Experimenten beobachteten dynamischen Streifen aus spin- und ladungsseparierten Bereichen wieder.

 

Weiterführende Literatur: - Von Ordnung zu Unordnung durch Quantenfluktuationen, Th. Vojta, Physik in unserer Zeit 1, 38 (2001). - Why high Tc is exciting, J. Zaanen, cond-mat/0103255 (2001). Dieser Artikel enthält eine kurze Einführung sowie weitere nützliche Referenzen auf etwas höherem Niveau.  - Quantum Criticallity: Competing Ground States in Low Dimensions, S. Sachdev, Science 288, 475 (2000).  - Quantum Phase Transitions, S. Sachdev, Cambridge United Press, New York (1999). Auszüge und weitere Literaturhinweise findet man auf der Homepage von S. Sachdev.  - Interacting Electrons and Quantum Magnetism, A. Auerbach, Springer Verlag (1998).